JavaScript RLE algorithm v2 - Sprite Tiles

This is the second post in my series about Run-Length Encoding (RLE) compression:

1. JavaScript Run-Length Encoding for Arcade Sprites
2. JavaScript RLE algorithm v2 - Sprite Tiles
3. JavaScript RLE algorithm v3 - Bit-Level RLE

In the previous post, I built a simple Run-Length Encoding in JavaScript to test how much it would compress retro videogame sprites with indirect color (palette color), of up to 16 colors.

In reality, sprites for many arcade and old consoles were stored as tiles, giant mosaics that games would then arrange in sprites and background layers. Chips for storing the game's data as ROM were also very restricted: You either had only a fixed limited amount, or each increment was very costly.

I know that some games had compression mechanisms to squeeze storage to the maximum, both for game data and assets/graphics [1], but they were custom solutions. But what if either the system had some built-in compression, or there was some SDK that provided compression tools and code? Would games in general benefit of this?

Weaknesses

In the first post, we saw that compressing full sprites gives up to slightly above 30% space-save for up to 4bpp (4 bits per plane). This is not bad, but it is not perfect; if the image has a non-optimal RLE-encodable pattern, it could occupy more space than the original. For example, the following is a zoomed-in and framed fragment of one of Street Fighter II backgrounds:

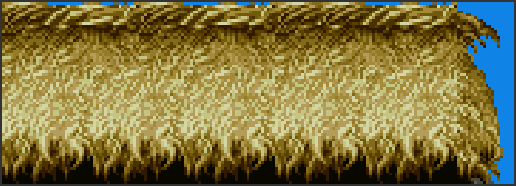
The raw image size is 11520 bytes, but the RLE encoded size goes up to 16232 bytes. That's a 41% size increase! I actually have cheated, because backgrounds are made up from tiles, and if you look closely, you'll notice that there is a repeating pattern in that image, but the main idea still stands: Certain images are more suited than others to RLE encoding.

There are usually two ways to avoid this: either employ an advanced bit-plane level RLE encoding (encode each "layer" or plane per color in the palette separately), or provide a way to apply RLE selectively per pixel (copy-repeat modes [2]).

The Experiment

Now that we've seen the biggest weakness of this compression algorithm, let's assume for the remainder of this experiment that, on average, the pros outweigh the cons, and that most images will save some space.

What I wanted to experiment with is: Considering that the storage format really is in tiles, and that today's computers are powerful, could we save more space by re-arranging how sprite tiles are stored? This is, if instead of just storing them as either horizontal or vertical "stripes", we somehow calculated a more optimal layout, would this yield better compression?

To get to this, I first slightly modified the source images to be multiples of 16x16 tiles. I then coded a tiler that both allows to split a raw image into an array of 16x16 tiles, and the opposite, combine tiles into a raw image. I finally added a tilerCompressor that works with a list of tiles, doing N permutations, each consisting of a random shuffling of the tiles, and then compresses the resulting image; if the result is better than the previous best, stores it. It is a very naive algorithm, but trivial to implement.

This is an example execution log, of a few thousands of iterations:

Raw image size: 6144
RLE encoded image size: 3618
Split into 24 tiles
New Best size: 3968
New Best size: 3966
New Best size: 3926
New Best size: 3902
New Best size: 3894
New Best size: 3892
New Best size: 3890
New Best size: 3888
New Best size: 3870
New Best size: 3866
New Best size: 3862
New Best size: 3842
New Best size: 3834
New Best size: 3832
New Best size: 3830
New Best size: 3816
New Best size: 3804
New Best size: 3800
New Best size: 3782
New Best size: 3780
Best permutation size: 3780
Best permutation ordering: [
  19, 2,  0, 12, 23,  9, 17, 15,
   4, 5, 16,  6, 11, 14,  7, 20,
   1, 3, 13,  8, 18, 21, 22, 10
]
Better than original sprite? false

I tested a few runs with 10 million iterations, and the best I could get was matching the original arrangement compression ratio (when tiles ended with the original arrangement).

This is how the HTML comparison page looks, now showing the best compressing permutation found:

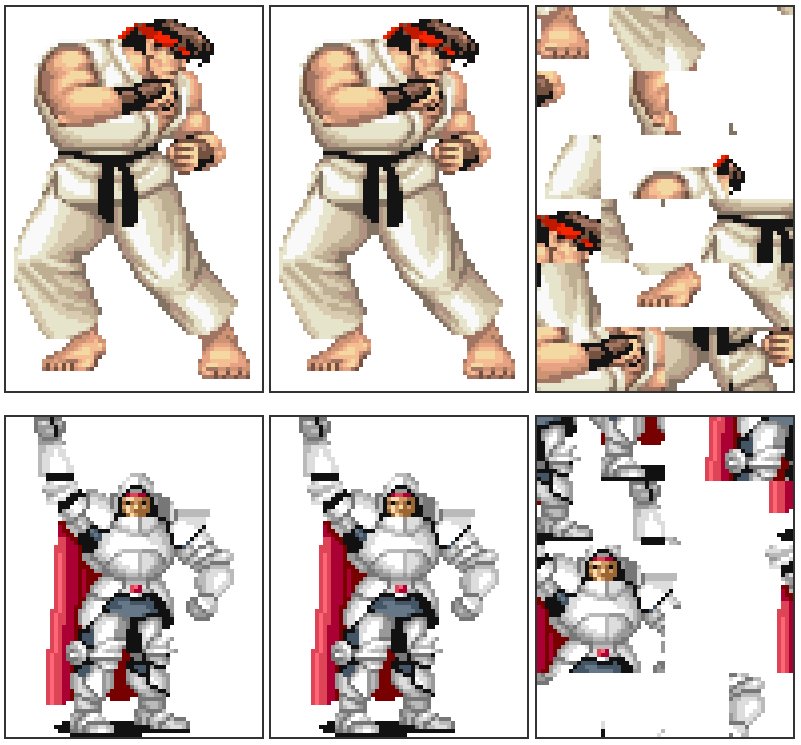
You can check the v2 implementation at my GitHub, inside the rle/v2 subfolder.

Potential Improvements

Regarding the randomness (ordering of tiles), I could have implemented some tile analysis and ordering heuristics (color frequencies, similar run-lengths, vertical vs horizontal stripping before randomization, ...), and in some cases it would improve the compression. I could have implemented some genetic algorithm (keep the previous mutation if it improved the compression ratio). I could also have kept a big hash map of already attempted combinations, and let it run until completion, but then, doing this brute-force approach for each sprite would be so overkill even today... I could have done many things, but I decided to keep it as a mere proof of concept.

I think that, in general, we can see that the tooling needs to be significantly complex to be effective. Graphic artists back in the day were excellent at drawing sprites, changing as few tiles as possible between animation frames, and even ordering them to maximize space usage [3]. So we can say that, probably, investing effort in a nice sprite editing tool (like the ones we have nowadays) would be more fruitful and generally applicable.

Regarding RLE, there are many approaches to go from the basic implementation towards a more optimized version: Delta encoding, bit-level RLE, Variable-length encoding, maybe applying Huffman encoding to the RLE output, trying reading the image bytes vertically instead of horizontally (at times gives better results)... While those and other more complex techniques can be applied, and were applied ad-hoc in some cases, it is also clear that simply RLE-encoding all the graphics ROM data wouldn't magically give extra space.

As often happens, there is no silver bullet that magically solves all the cases.

The End?

I initially planned to stop here. I can draw some quick conclusions and call it a day:

• RLE compression can save around 30% space
• Is not worth trying to rearrange the tiles; as long as they belong to the same sprite will compress nicely with RLE
• When image patterns don't help with RLE, it's better to not use RLE, or use it selectively

Instead, I've decided that I want to play with the bit-level RLE encoding, because while researching for the experiment I found that things get more interesting when you go down to bits. It will still be a basic implementation, and I will switch to GameBoy sprites (because they only contain 4 colors, which simplifies things), but there will definitely be a third post around this topic soon.

[1] GameBoy's Zelda: A Link to the past has a very creative map storage format. And Pokemon has a highly space-optimized bit-level RLE compression algorithm for all sprite tiles.

[2] This is typically done by switching to bit-level RLE. The first bit of each data point indicates if the mode is copy (representing a single palette index pixel) or repeat (representing an N-times repetition of a palette index color).

[3] If you want to see how much work went into manually organizing sprite sheets, check this amazing post: CPSS: The Capcom Sheets Explorer.